« Back to AP Physics Guide / Unit 1: Kinematics
AP Physics 1: Projectile Motion & Vectors
1. Breaking Down Vectors
Before solving projectile problems, you must be able to split a diagonal velocity vector into its components. In AP Physics 1, we use trigonometry (SOH CAH TOA) to do this.

 ) into its horizontal (
) into its horizontal ( ) and vertical (
) and vertical ( ) components using trigonometry.
) components using trigonometry.- Horizontal Component (vx):

- Vertical Component (vy):

Calculus Note: AP Physics 1 does not use unit vectors (![]() ) or dot products. Stick to x and y components.
) or dot products. Stick to x and y components.
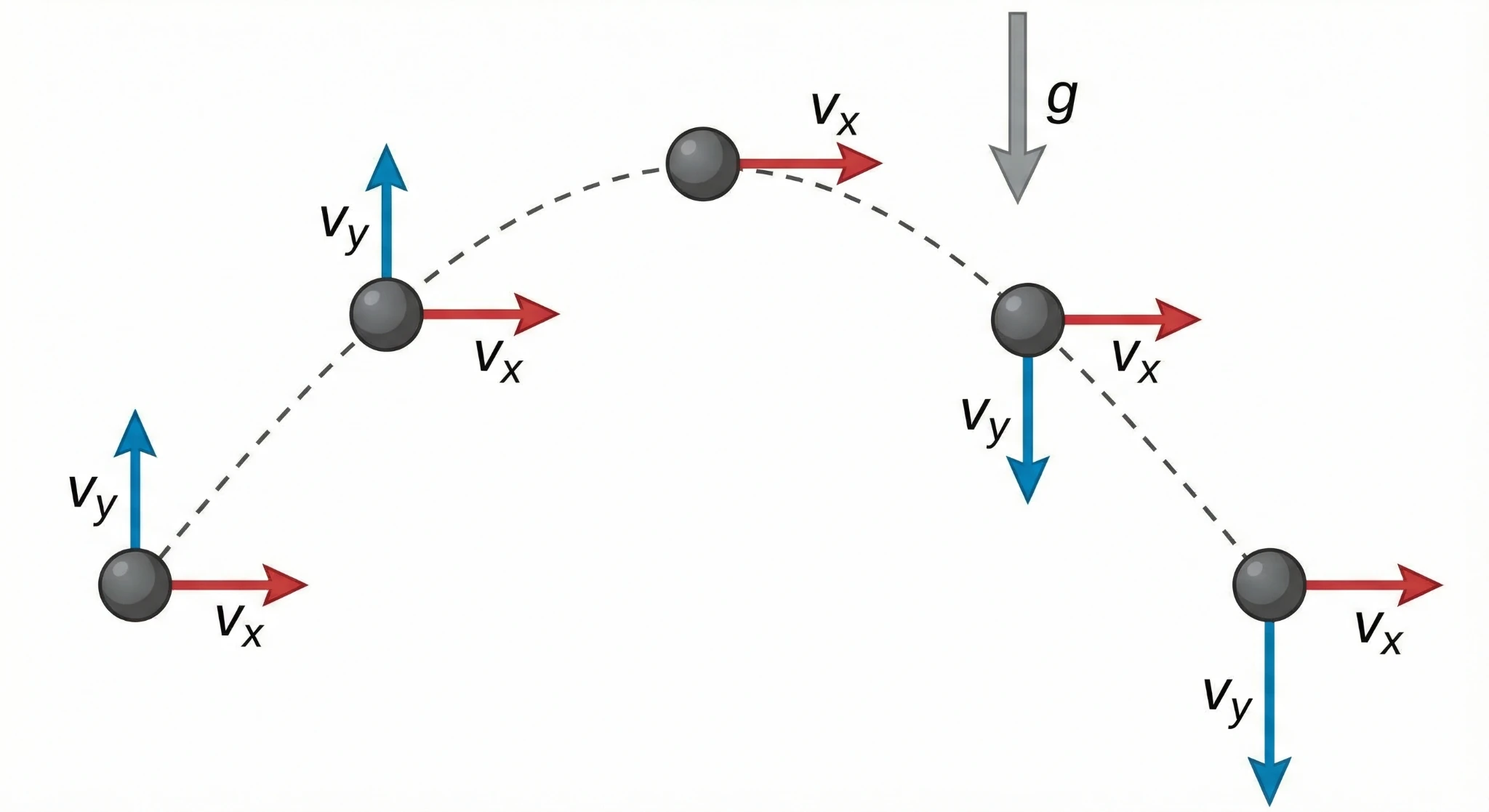
2. The Two Rules of Projectile Motion
If you memorize nothing else, memorize this table. This is how you set up every FRQ.
| Axis | Acceleration | Velocity Behavior | Equation to Use |
|---|---|---|---|
| Horizontal (X) | Constant Velocity | ||
| Vertical (Y) | Changing (Free Fall) | Use “Big 3” Kinematics Equations |
The Bridge: The only variable that is the same for both X and Y sides is Time (t).

 ).
).3. Three Scenarios You Will See

A. Horizontal Launch
Object thrown straight off a cliff.
- Initial

- Initial

- Time depends only on height!
B. Angled Launch (Ground-to-Ground)
Object kicked like a soccer ball.
- At the peak height,
 (but
(but  is still there!)
is still there!) - Time up = Time down (if landing at same height).
4. AP-Style Concept Check
Try this “Paragraph Length Response” style question. No numbers allowed!
Question: Two identical balls are released from the top of a cliff at the same time. Ball A is dropped from rest. Ball B is thrown horizontally outward with speed ![]() . Which ball hits the ground first? Justify your answer.
. Which ball hits the ground first? Justify your answer.
Click to see the Answer
Answer: They hit at the same time.
Reasoning: The vertical motion of an object is independent of its horizontal motion. Both balls start with an initial vertical velocity of zero (![]() ) and fall the same vertical distance (
) and fall the same vertical distance (![]() ) under the same acceleration due to gravity (
) under the same acceleration due to gravity (![]() ). Therefore, according to the equation
). Therefore, according to the equation ![]() , the time
, the time ![]() to fall must be identical for both.
to fall must be identical for both.
5. AP-Style Derivation Practice
On the AP Exam, you are often asked to derive equations using only variables. Practice these three common scenarios. Do not memorize the final answers; memorize the steps!
Derivation 1: Total Horizontal Range (![]() )
)
Find the horizontal distance derived in terms of ![]() ,
, ![]() , and
, and ![]() .
.
Click to see Step-by-Step Derivation
Step 1: Horizontal Motion
![]() (Eq 1)
(Eq 1)
Step 2: Vertical Motion (Find Time)
Total displacement ![]() .
.
![]() (Eq 2)
(Eq 2)
Step 3: Substitute and Solve
![]()
Derivation 2: Maximum Height (![]() )
)
Find the peak height derived in terms of ![]() ,
, ![]() , and
, and ![]() .
.
Click to see Step-by-Step Derivation
The Key Concept:
At the very peak of the flight, the vertical velocity (![]() ) is zero.
) is zero.
Step 1: Choose the Right Equation
We don’t know time, so use the time-independent equation:
![]()
Step 2: Substitute Variables
Final vertical velocity ![]()
Initial vertical velocity ![]()
Acceleration ![]()
Displacement ![]()
Step 3: Solve for ![]()
![]()
![]()
![]()
Derivation 3: Equation of Trajectory (Path)
Prove that the path is a parabola by finding ![]() as a function of
as a function of ![]() .
.
Click to see Step-by-Step Derivation
Goal: Eliminate time (![]() ) from the equations.
) from the equations.
Step 1: Solve for ![]() using Horizontal Equation
using Horizontal Equation
![]()
![]() (Eq A)
(Eq A)
Step 2: Plug ![]() into the Vertical Equation
into the Vertical Equation
![]()
![]()
Step 3: Simplify
Use the identity ![]() :
:
![]()
Notice that this follows the form ![]() , which is mathematically a downward-opening parabola.
, which is mathematically a downward-opening parabola.
6. Don’t Lose Easy Points!
❌ The “Velocity at Peak” Trap
Mistake: Saying velocity is zero at the peak.
Truth: Only the vertical velocity (![]() ) is zero. The horizontal velocity (
) is zero. The horizontal velocity (![]() ) is still there!
) is still there!
❌ The “Acceleration” Trap
Mistake: Saying acceleration is zero at the peak.
Truth: Acceleration is always ![]() downwards, even at the very top.
downwards, even at the very top.
Ready for the next step?
Go to Unit 2: Forces »