Friction: Static vs. Kinetic & The “Funky” Formula

The Golden Rule: Friction always acts parallel to the surface and opposes slipping (not necessarily motion!).

1. The “Funky” Formula

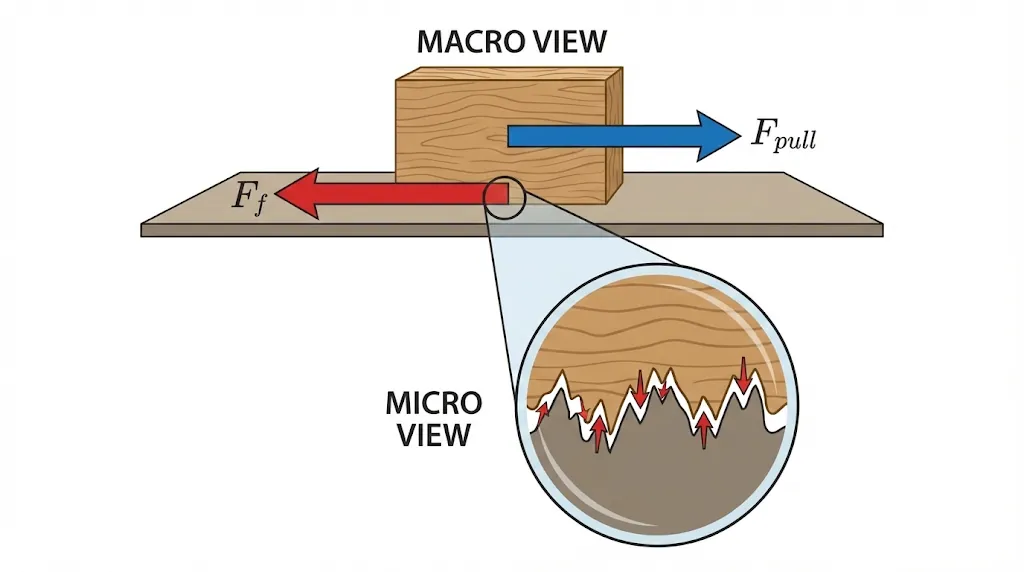
Friction depends on only two things: how rough the surfaces are and how hard they are smashed together.

$|F_f| \le \mu |F_N|$

1. The Coefficient of Friction ( $\mu$ ): A number between 0 and 1 that rates “roughness.”
(Ice on Ice $\approx 0.05$ , Rubber on Concrete $\approx 0.8$ ). It has NO units!
2. Normal Force ( $F_N$ ): How hard the surfaces press against each other.
(Heavier object = More $F_N$ = More Friction).

Notice that Surface Area is NOT in the equation! Sliding a brick on its wide face or its skinny side produces the exact same friction.

2. Static vs. Kinetic: The Battle

There are two types of friction, and they behave very differently.

Physics graph of Friction Force versus Applied Force showing a diagonal static line rising to a peak, then dropping to a lower constant kinetic horizontal line. — The “Stick-Slip” phenomenon. Notice how the graph **drops** once the object starts moving. It is harder to *start* motion (Static) than to *maintain* it (Kinetic).

Static Friction ( $F_{s}$ )

“Sticking” Force

Acts when object is NOT sliding.
It’s smart! It adjusts its strength to exactly match the push, up to a maximum limit.
Equation: $F_s \le \mu_s F_N$

Kinetic Friction ( $F_{k}$ )

“Sliding” Force

Acts when object IS sliding.
It’s dumb! It is always the same constant value, no matter how fast you slide.
Equation: $F_k = \mu_k F_N$

Crucial Fact: $\mu_s > \mu_k$ . It is always harder to start moving something (Static) than to keep it moving (Kinetic). This is why the graph “drops” once you start sliding.

3. The Direction Trap: Walking

Does friction always oppose motion? NO! Friction opposes slipping.

Example: Walking.
When you walk, your foot tries to slip backward. Therefore, Static Friction pushes your foot FORWARD. Without friction, you would slip in place (like a cartoon character on ice).

4. AP-Style Practice Questions

Question 1 (The Magic Number): A $10 \, \text{kg}$ block rests on a floor. The coefficient of static friction is $0.4$ . You push the block horizontally with $30 \, \text{N}$ of force. What is the friction force?

▶ Click for Answer

Answer: $30 \, \text{N}$ (Not 40 N!)

Reasoning:
Step 1: Calculate the Max Limit.
$F_{s,max} = \mu_s F_N = (0.4)(10 \times 10) = 40 \, \text{N}$ .
Step 2: Check your push.
You are pushing with $30 \, \text{N}$ , which is less than the limit ( $40 \, \text{N}$ ).
Therefore, the block does not move, and Static Friction simply matches your push to cancel it out.