« Back to AP Physics Guide / AP Physics 1 – Unit 3: Orbits & Kepler’s Laws (Topics 3.6-3.8)

AP Physics 1 – Orbits & Kepler’s Laws: v = √(GM/r) and T² ∝ r³

From satellites to moons: Objects in circular orbits are essentially falling forever. In this final guide for Unit 3, we derive the orbital velocity equation, prove Kepler’s Third Law, and solve AP-style orbit problems.

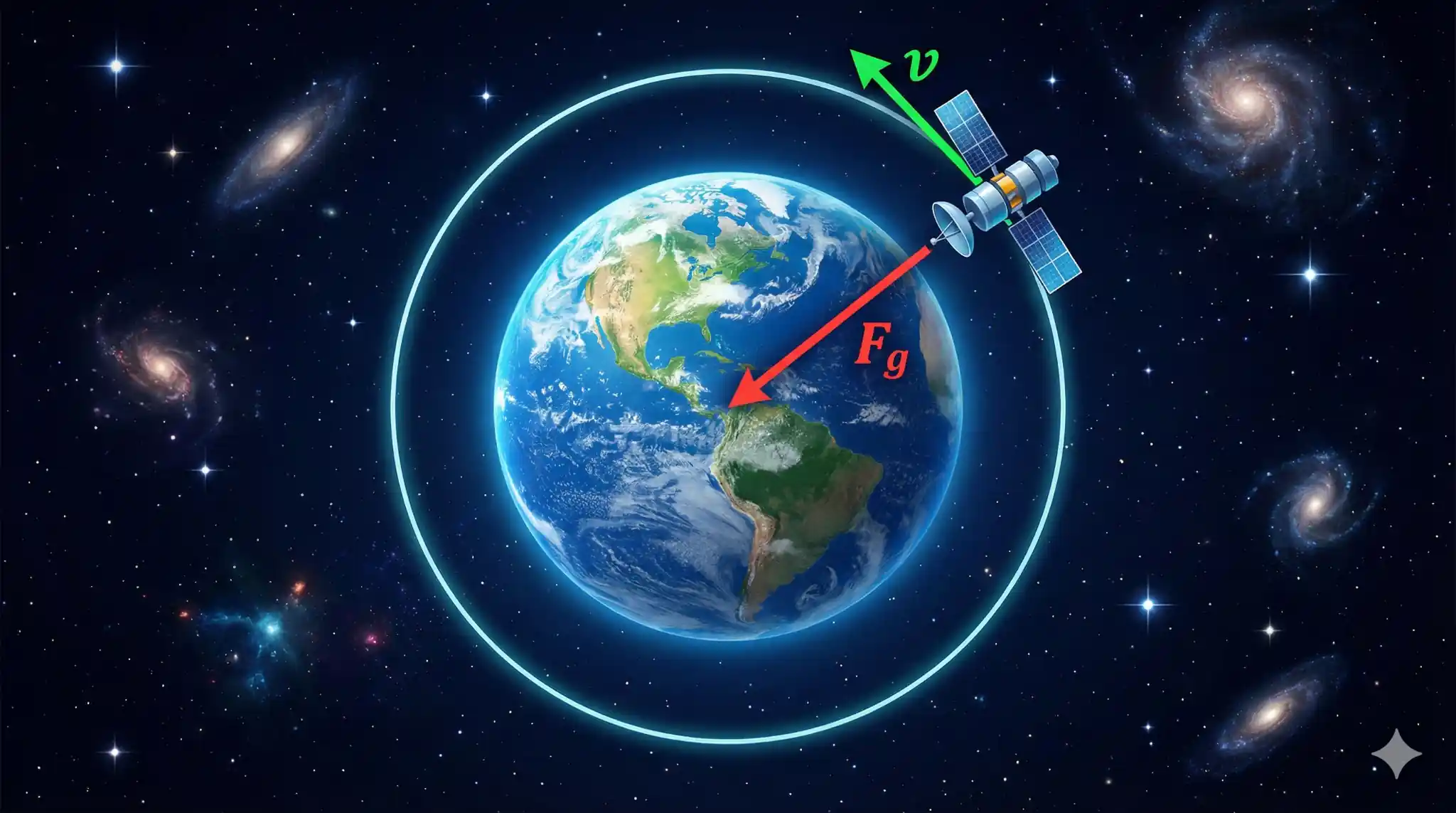
1. Orbital Velocity: The Gravity-Centripetal Balance

A satellite stays in orbit because the Gravitational Force pulls it inward with exactly the strength needed to provide the Centripetal Force.

The Derivation You Must Know

$F_g = F_c$
$\dfrac{GMm}{r^2} = \dfrac{mv^2}{r}$

Solve for v:
$v_{orbit} = \sqrt{\dfrac{GM}{r}}$

Note: Little mass $m$ (the satellite) cancels out! Speed depends only on the planet mass $M$ and radius $r$ .

Closer Orbit (Small r)
Gravity is stronger, so you must move FASTER to stay in orbit.

$v \uparrow$

Heavier Planet (Big M)
Gravity is stronger, so you must move FASTER.

$v \uparrow$

2. Orbital Period: Kepler’s Third Law

How long does one full orbit take? By combining velocity with the circle circumference formula ( $v = 2\pi r / T$ ), we find a powerful relationship.

Diagram showing satellite in circular orbit with gravitational force providing centripetal force. — **The Connection:** $T = \dfrac{2\pi r}{v}$ . Substituting $v = \sqrt{GM/r}$ gives us $T^2 \propto r^3$ .

⚠️ The “T-Squared, R-Cubed” Rule:
$T^2 = \left( \frac{4\pi^2}{GM} \right) r^3$
This means if you know the radius, you know the period. They are locked together.

3. Kepler’s Three Laws (Summary)

Diagram of Kepler's first law showing a planet in an elliptical orbit with the star at one focus. — **1st Law:** Orbits are ellipses. The star is at one focus, not the center.

1st Law (The Law of Ellipses): All planets move in elliptical orbits, with the sun at one focus. (Note: In AP Physics 1, we usually approximate orbits as perfect circles to make the math easier).

Diagram of Kepler's second law showing a planet sweeping out equal areas in equal times, moving faster near the star. — **2nd Law:** Equal areas in equal time means the planet moves faster when closer to the star.

2nd Law (The Law of Equal Areas): A line that connects a planet to the sun sweeps out equal areas in equal times.
Physics Reason: This is a direct consequence of the Conservation of Angular Momentum. As the radius $r$ decreases, speed $v$ must increase to keep angular momentum $L = mvr$ constant.
3rd Law (The Law of Harmonics): The square of the period of any planet is proportional to the cube of the semimajor axis of its orbit ( $T^2 \propto r^3$ ).