Vector Algebra – Advanced Physics

Vector Algebra

(Advanced Physics)

Quick reference
• Magnitude: $A = \sqrt{A_x^2 + A_y^2 + A_z^2}$
• Dot product: $\vec{A}\cdot\vec{B} = A_xB_x + A_yB_y + A_zB_z$
• Cross product magnitude: $|\vec{A}\times\vec{B}| = AB\sin\theta$

Diagram of vectors represented as arrows showing magnitude and direction — Vectors encode both magnitude and direction — essential for describing physical reality.

1. Why Physics Needs Vectors

Physics describes nature in space. In space, direction matters. A single number is often insufficient to describe physical reality.

A vector is not just an arrow. It is a quantity that remains meaningful when space is rotated or shifted.

2. Scalars vs Vectors — A Deeper Meaning

Scalars remain unchanged under rotation. Vectors change components but preserve physical magnitude.

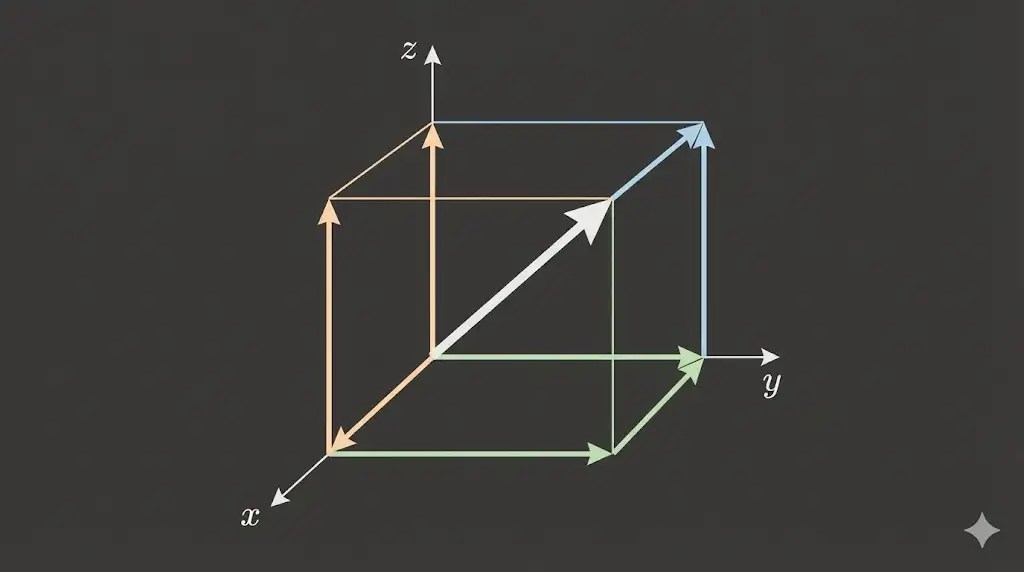
3. Representing a Vector

In calculations, a vector is usually represented by its components along three perpendicular axes. The components change under rotation, but the underlying geometric vector does not.

$\vec{A} = A_x \hat{i} + A_y \hat{j} + A_z \hat{k}$

Diagram of a vector resolved into x y and z components — Any vector can be resolved along mutually perpendicular coordinate axes.

4. Dot Product — Measuring Alignment

The dot product answers a simple but powerful question: how much of one vector actually contributes along another?

The dot product compresses two vectors into a scalar that tells how strongly they point in the same direction. It is maximised when vectors are parallel and zero when they are perpendicular.

Diagram showing projection of one vector onto another for dot product — The dot product measures how strongly one vector aligns with another.

$\vec{A}\cdot\vec{B} = AB\cos\theta$

5. Cross Product — Measuring Rotation

While the dot product measures alignment, the cross product measures rotation.

The cross product produces a new vector perpendicular to the plane of $\vec{A}$ and $\vec{B}$ , encoding both the axis and strength of a rotational effect.

$\vec{A}\times\vec{B} = AB\sin\theta\,\hat{n}$

The direction of the cross product is perpendicular to the plane formed by the two vectors and is determined using the right-hand rule.

Diagram illustrating the right hand rule for cross product direction — The direction of the cross product follows the right-hand rule.

Direction alone is not the full story. The cross product exists because nature often responds through rotation.

Diagram showing torque as a cross product of position vector and force — Cross products naturally describe rotational effects such as torque.

6. Triple Products

Triple products combine dot and cross products to capture signed volume and mixed rotational–alignment effects in three dimensions.

Diagram showing volume of a parallelepiped formed by three vectors — The scalar triple product represents the volume enclosed by three vectors.

$\vec{A}\cdot(\vec{B}\times\vec{C})$

Practice Problems

Level 1 — Conceptual

Why does the dot product measure work done?

Solution

Because it selects the component of force along displacement.

Why is the cross product linked to rotation?

Solution

Because it measures the tendency to produce angular motion.

Can a vector have magnitude but no direction?

Solution

No. Direction is an essential attribute of a vector.

Level 2 — Analytical (Component-Level)

If $\vec{A}\cdot\vec{B}=AB$ , what is the angle between them?

Solution

Zero degrees; vectors are parallel and aligned.

Under what condition does torque vanish even if force is non-zero?

Solution

When the line of action passes through the pivot.

Show that dot product is distributive over addition.

Solution

Let $\vec{A} = (A_x, A_y, A_z)$ , $\vec{B} = (B_x, B_y, B_z)$ , $\vec{C} = (C_x, C_y, C_z)$ .
Then $\vec{A}\cdot(\vec{B}+\vec{C}) = A_x(B_x+C_x) + A_y(B_y+C_y) + A_z(B_z+C_z)$ .
Grouping terms gives $(A_xB_x + A_yB_y + A_zB_z) + (A_xC_x + A_yC_y + A_zC_z)$ .
So $\vec{A}\cdot(\vec{B}+\vec{C}) = \vec{A}\cdot\vec{B} + \vec{A}\cdot\vec{C}$ .

Level 3 — Advanced (Physical Reasoning)

Explain why vector multiplication is not associative using physical reasoning.

Solution

Changing grouping alters direction and plane of the result.

What physical insight does a zero scalar triple product give?

Solution

The vectors lie in a plane and enclose no volume.

Why does angular momentum use a cross product, not dot product?

Solution

Because angular momentum depends on rotational tendency, not alignment.

Next → Relative Motion