« Back to AP Physics Guide / AP Physics 1 – Unit 4: Conservation of Energy

AP Physics 1: Conservation of Energy

This is the single most powerful problem-solving tool in AP Physics 1. If you can define a system where energy is conserved, you can solve complex motion problems without ever calculating acceleration or time.

AP Physics 1 Unit 4 (Conservation): This topic appears in many free-response questions where you must justify your steps with energy bar charts or equations.

1. The Law of Conservation

The law states that energy cannot be created or destroyed, only transferred or transformed. For a closed system (where no energy enters or leaves), the total mechanical energy remains constant.

$E_i = E_f$

Initial Mechanical Energy = Final Mechanical Energy

This means if you drop a ball, the gravitational potential energy $U_g$ it loses is perfectly converted into kinetic energy $K$ .

$U_{gi} + K_i = U_{gf} + K_f$

2. The “Master Equation” (Open Systems)

Real life has friction. Friction and air resistance are non-conservative forces. They take mechanical energy out of your system and turn it into heat (thermal energy).

When friction is present, we modify the conservation equation:

Diagram showing Initial Energy plus Work by Non-Conservative Forces equals Final Energy.

The Master Equation: Start with what you have $E_i$ , add the work done by non-conservative forces $W_{nc}$ , and that equals what you have at the end $E_f$ .

$E_i + W_{nc} = E_f$

Often written as: $E_i - \lvert W_{\text{friction}} \rvert = E_f$

Here $W_{nc}$ (work by non-conservative forces) is usually negative because friction acts opposite the motion.

3. How to Solve Rollercoaster Problems

The classic AP Physics problem involves a rollercoaster, pendulum, or skateboarder in a bowl. Follow these three steps to solve most conservation-of-energy questions.

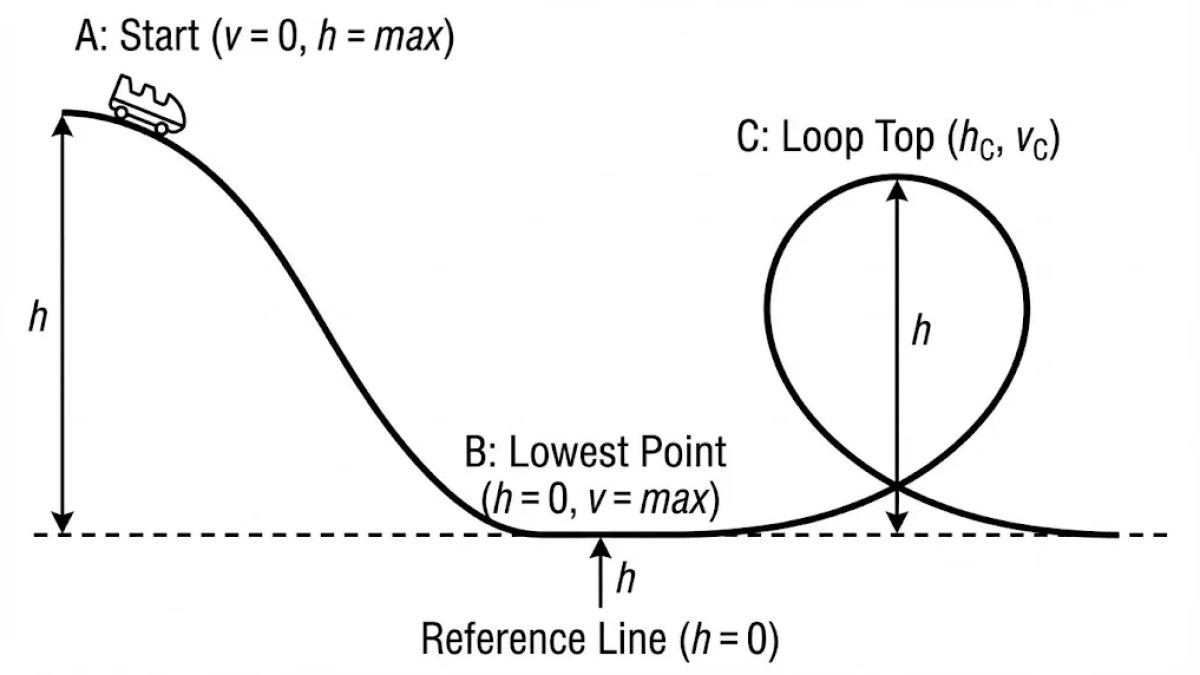
Roller coaster diagram with Point A, B, and C labels.

Setup is Key: Always define your zero-height line $h = 0$ at the lowest point (Point B) to simplify the math.

Step 1: Set the $h = 0$ Line

Draw a horizontal dashed line at the lowest point the object reaches (Point B). At this line, $U_g = 0$ .

Step 2: Identify Energy at Each Point

Point A (Top): If it starts from rest, energy is all $U_g$ . If it has speed, energy is $U_g + K$ .
Point B (Bottom): Height is zero, so energy is all $K$ .
Point C (Loop or crest): Has height and speed, so energy is $U_g + K$ .

Step 3: Write and Solve the Equation

If friction is negligible: Energy at A = Energy at B.

$m g h_A = \tfrac{1}{2} m v_B^2$

Notice mass $m$ cancels out. The speed at the bottom does not depend on the mass of the cart.

Quick Example

Q: A 500 kg rollercoaster car starts from rest at height $h = 20\ \text{m}$ (no friction). What is its speed at the bottom?

Solution: $mgh = \tfrac{1}{2} mv^2 \Rightarrow gh = \tfrac{1}{2} v^2$ .

$v = \sqrt{2 g h} = \sqrt{2 \times 9.8 \times 20} \approx 19.8\ \text{m/s}$ .

⚠️ Common Mistake: Do not double-count gravity. Either use gravitational potential energy $U_g$ in your energy equation, or treat gravity as a force doing work, but not both.

Unit 4 Complete!

You have mastered Work, Power, and Conservation of Energy. Next up in AP Physics 1 is the other big conserved quantity in mechanics: Momentum.

Next Unit: Momentum & Impulse (Unit 5) →