January 17, 2026

Tension, Pulleys & Inclined Planes (Systems)

Free body diagram of a block on a ramp with the X-axis rotated parallel to the surface. Gravity ($mg$) is broken into two dashed components: $mg \sin \theta$ pointing down the slope and $mg \cos \theta$ pointing into the slope.

« Back to AP Guide / Unit 2: Dynamics

Tension, Pulleys & Inclined Planes (Systems)

The Secret: In these problems, you usually don’t solve for just one object. You look at the Whole System.

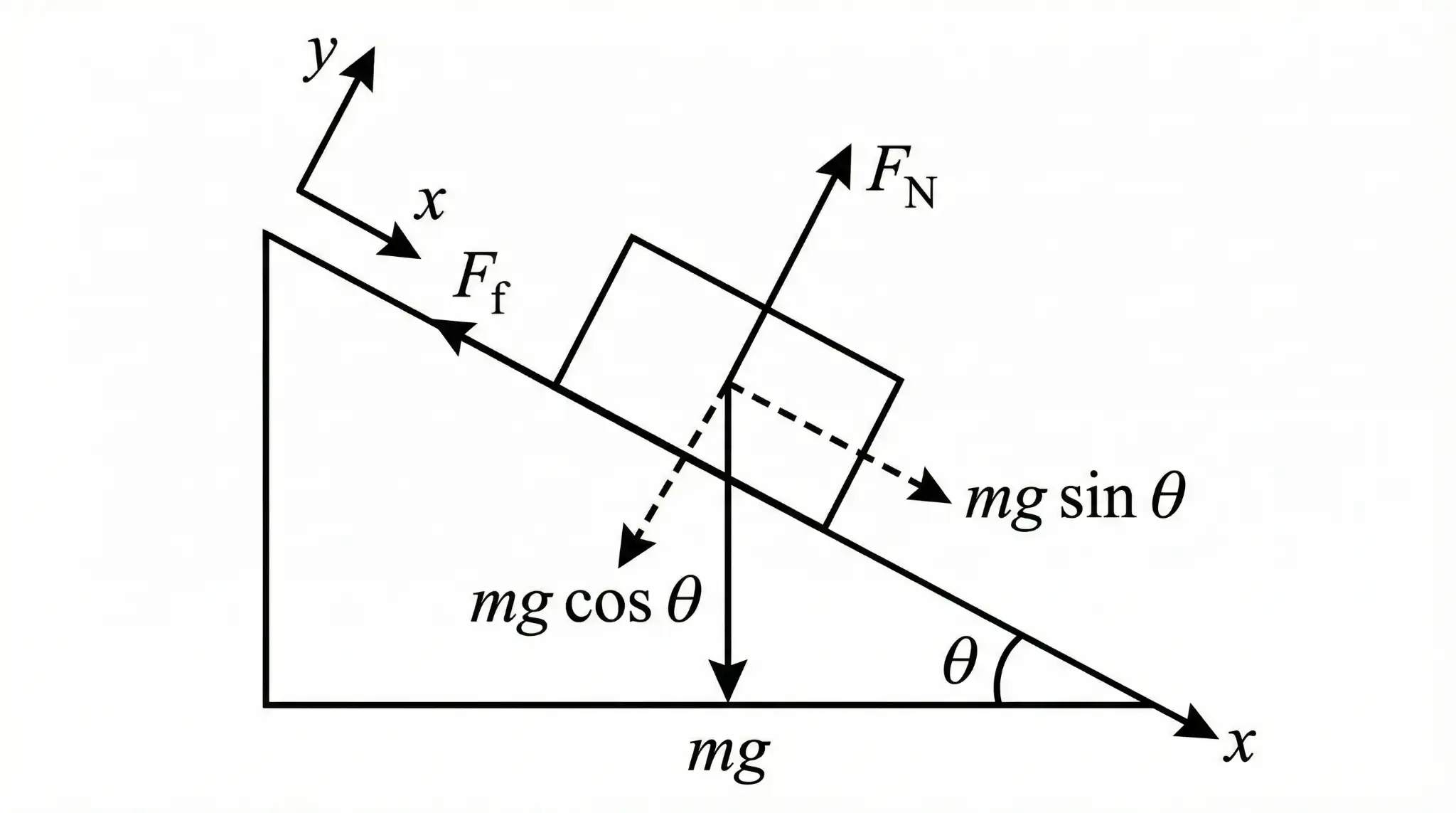
1. Inclined Planes (The “Tilt” Trick)

Gravity always pulls straight down, but ramps are diagonal. The fix? Rotate your axes!

Free body diagram of a block on an inclined plane showing gravity components mg sin theta and mg cos theta.
Notice how we rotate the X-axis to match the slope. Gravity is the ONLY force we have to break into components.

The Magic Components

You must memorize how to break Gravity (mg) into X and Y parts:

  • 1. The “Slider” (F_{gx}): pulls the block down the ramp.
    F_{gx} = mg \sin(\theta)
  • 2. The “Presser” (F_{gy}): pushes the block into the ramp.
    F_{gy} = mg \cos(\theta)

Memory Aid: “Sin is Sliding down the ramp.”

2. Tension & Pulley Systems

When two objects are connected by a rope (like an Atwood Machine), they move as One Giant Object.

Atwood machine pulley system diagram showing forces on two hanging masses.
The Atwood Machine. The heavier mass pulls the lighter mass up. They share the same acceleration magnitude.

The “System” Shortcut

Instead of writing two separate equations, do this:

a_{system} = \frac{\text{Net Force}}{\text{Total Mass}}

Example: A 5kg block pulls a 2kg block. Total Mass = 7kg.
Net Force = The tug-of-war between weights.
Internal Forces (Tension) CANCEL OUT. Ignore them for this step!

3. AP-Style Practice Questions

Question 1 (The Ice Ramp): A block slides down a frictionless ramp inclined at 30^\circ. What is its acceleration?

▶ Click for Answer

Answer: 5 \, \text{m/s}^2

Reasoning:
1. Identify Force: The only force pulling it down is mg \sin(30^\circ).
2. Apply F=ma:
mg \sin(30^\circ) = ma
Mass cancels out! a = g \sin(30^\circ).
a = (10)(0.5) = 5 \, \text{m/s}^2.

Question 2 (The Atwood Machine): A 6 \, \text{kg} mass and a 4 \, \text{kg} mass are hung over a pulley. What is the acceleration of the system?

▶ Click for Answer

Answer: 2 \, \text{m/s}^2

Reasoning:
Step 1: Total Mass = 6 + 4 = 10 \, \text{kg}.
Step 2: Net Force (Tug of War) = 60N - 40N = 20N.
Step 3: Solve
a = \frac{F_{net}}{m_{total}} = \frac{20}{10} = 2 \, \text{m/s}^2.

You Finished Unit 2!

You have mastered Forces, Friction, and Systems. Ready for the next challenge?