« Back to AP Physics Guide / AP Physics 1 – Unit 3: Universal Gravitation
AP Physics 1 – Universal Gravitation: Force, Field & How g Changes
Newton’s Big Idea: The force that makes an apple fall is the same force that keeps the Moon in orbit.
In this guide (Topics 3.4 & 3.5), we break down Newton’s Law of Universal Gravitation,
the difference between ![]() and
and ![]() , and how to read the famous “Gravity Graph” that appears on the AP Exam.
, and how to read the famous “Gravity Graph” that appears on the AP Exam.
1. Newton’s Law of Universal Gravitation
Every object in the universe attracts every other object. This force is proportional to their masses and inversely proportional to the square of the distance between them.
The “Universal” Equation
![]()
 : Gravitational Force (Newtons). Always attractive.
: Gravitational Force (Newtons). Always attractive. : The two masses (kg).
: The two masses (kg). : Distance between the centers of the masses (meters).
: Distance between the centers of the masses (meters). : The Universal Constant (
: The Universal Constant ( ).
).
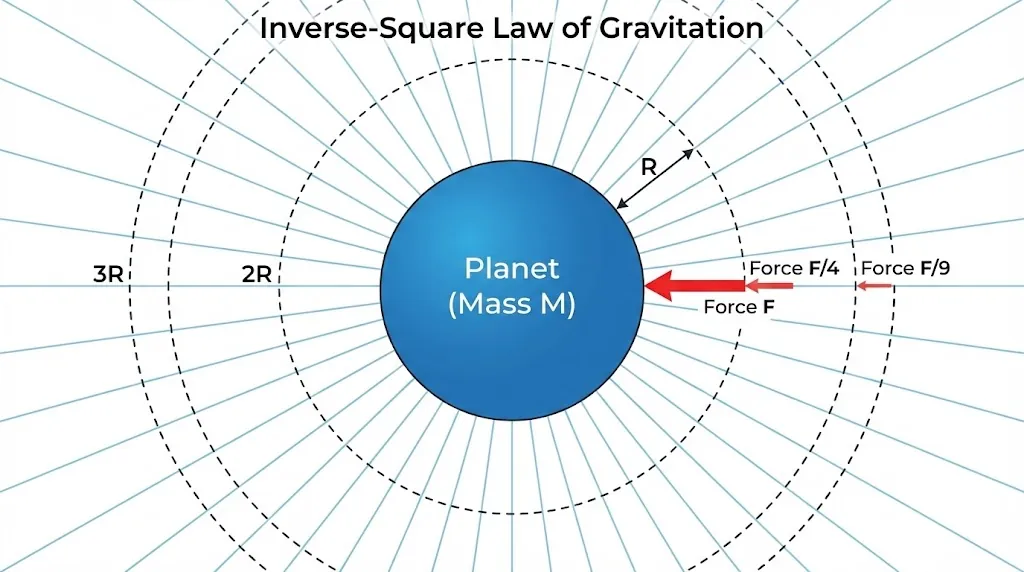
2. The Inverse Square Law
Gravity is an “inverse square” force. This means if you move twice as far away, the force drops by a factor of four.

 )
)  Quarter the force (
Quarter the force ( ).
).
![]()
![]()
![]()
3. Gravitational Field Strength ( )
)
We say ![]() on Earth, but what about on Mars or in orbit? By setting
on Earth, but what about on Mars or in orbit? By setting ![]() , we can solve for the field strength anywhere:
, we can solve for the field strength anywhere:
![]()
This tells us:
- Mass (
 ): Heavier planets create stronger fields.
): Heavier planets create stronger fields. - Distance (
 ): The further you are, the weaker
): The further you are, the weaker  gets (inverse-square).
gets (inverse-square).
g ≈ 9.8 m/s² is the local value near Earth’s surface.Global formula:
4. Graphing Gravity: Inside vs. Outside
This is a favorite AP Exam question (Topic 3.4). How does gravity change as you travel from the center of a planet out to deep space?

- Inside (
 ):
):
Gravity increases linearly. As you move out, there is “more planet” underneath you. ( )
) - The Surface (
 ):
):
Gravity is at its maximum. - Outside (
 ):
):
Gravity decreases as the inverse square. ( )
)
5. Concept Check: Types of Mass
Inertial Mass: Resistance to acceleration (![]() ).
).
Gravitational Mass: How strongly it interacts with gravity (![]() ).
).
Key Idea: Experiments show these two are identical. This is why all objects fall at the same rate regardless of mass!
6. AP Practice Problems
Problem 1: Planet X
Planet X has twice the mass (![]() ) and twice the radius (
) and twice the radius (![]() ) of Earth. What is the surface gravity (
) of Earth. What is the surface gravity (![]() ) on Planet X compared to Earth?
) on Planet X compared to Earth?
Click to see answer
Answer: ![]() (Half as strong)
(Half as strong)
Use the formula ![]() .
.
![]()
The larger radius weakens gravity more than the extra mass strengthens it.
Problem 2: The Satellite Ratio
A satellite moves from Earth’s surface (![]() ) to an orbit at distance
) to an orbit at distance ![]() from the center. How does the force of gravity change?
from the center. How does the force of gravity change?
Click to see answer
Answer: It becomes ![]() as strong.
as strong.
The distance doubled (![]() ).
).
Since ![]() , doubling distance divides force by
, doubling distance divides force by ![]() .
.
7. More AP Physics 1 Practice Problems
Problem 3: g vs r Graph
On the g vs r graph above, where is the gravitational field strength maximum?
Click to see answer
Answer: At the surface (![]() )
)
Inside: ![]() increases linearly. Outside:
increases linearly. Outside: ![]() decreases as
decreases as ![]() . Maximum is at
. Maximum is at ![]() .
.
Problem 4: Jupiter vs Earth
Jupiter has 318 times Earth’s mass but 11 times Earth’s radius. What is Jupiter’s surface gravity compared to Earth’s?
Click to see answer
Answer: ![]() (2.6 times stronger)
(2.6 times stronger)
![]()
Problem 5: Inertial vs Gravitational Mass
Two objects (1 kg and 10 kg) are dropped from the same height in a vacuum. Why do they hit the ground together?
Click to see answer
Answer: Inertial mass = Gravitational mass (equivalence principle)
Both experience the same ![]() . Heavier object’s greater inertia is exactly balanced by greater gravitational pull.
. Heavier object’s greater inertia is exactly balanced by greater gravitational pull.