CBSE Class 12 › Unit V: Electromagnetic Waves

Electromagnetic Waves

NCERT Chapter 8 • Displacement Current & The EM Spectrum

NCERT 2025–26 Unit V • ~4 Marks JEE Main • 1 Question

1. Displacement Current

Maxwell found an inconsistency in Ampere’s Circuital Law when applied to a capacitor charging circuit. To resolve this, he introduced the concept of **Displacement Current**.

For a deep dive into how this current “flows” through the gap between capacitor plates, read our detailed guide: What is Displacement Current? (Concepts Explained).

Diagram showing the inconsistency in Ampere's Law that led to the discovery of displacement current. — Current passes through surface S1 but not S2, violating Ampere’s Law.

Derivation: Displacement Current Formula 3 Marks

Step 1: Electric Flux
Consider a parallel plate capacitor with area $A$ and charge $Q$ .
The electric field between plates is $E = \dfrac{\sigma}{\epsilon_0} = \dfrac{Q}{A \epsilon_0}$ .
Flux $\Phi_E = E \cdot A = \dfrac{Q}{\epsilon_0}$ .

Step 2: Rate of Change
Differentiating with respect to time:
$\dfrac{d\Phi_E}{dt} = \dfrac{1}{\epsilon_0} \dfrac{dQ}{dt}$ .

Step 3: Definition of Current
We know $\dfrac{dQ}{dt} = I$ (the conduction current).
Rearranging the equation: $I = \epsilon_0 \dfrac{d\Phi_E}{dt}$ .

Step 4: Conclusion
This missing current term is called Displacement Current ( $I_d$ ).
$I_d = \epsilon_0 \dfrac{d\Phi_E}{dt}$ .

Total Current:

The generalized Ampere’s Law uses the sum of conduction and displacement currents:
$I = I_c + I_d$ .

2. Maxwell’s Equations

Maxwell unified electricity and magnetism into a set of four equations. These are the fundamental laws of electromagnetism.

1. Gauss’s Law (Electrostatics):
$\oint \vec{E} \cdot d\vec{A} = \dfrac{Q_{in}}{\epsilon_0}$

2. Gauss’s Law (Magnetism):
$\oint \vec{B} \cdot d\vec{A} = 0$ (No magnetic monopoles)

3. Faraday’s Law:
$\oint \vec{E} \cdot d\vec{l} = - \dfrac{d\Phi_B}{dt}$

4. Ampere-Maxwell Law:
$\oint \vec{B} \cdot d\vec{l} = \mu_0 I_c + \mu_0 \epsilon_0 \dfrac{d\Phi_E}{dt}$

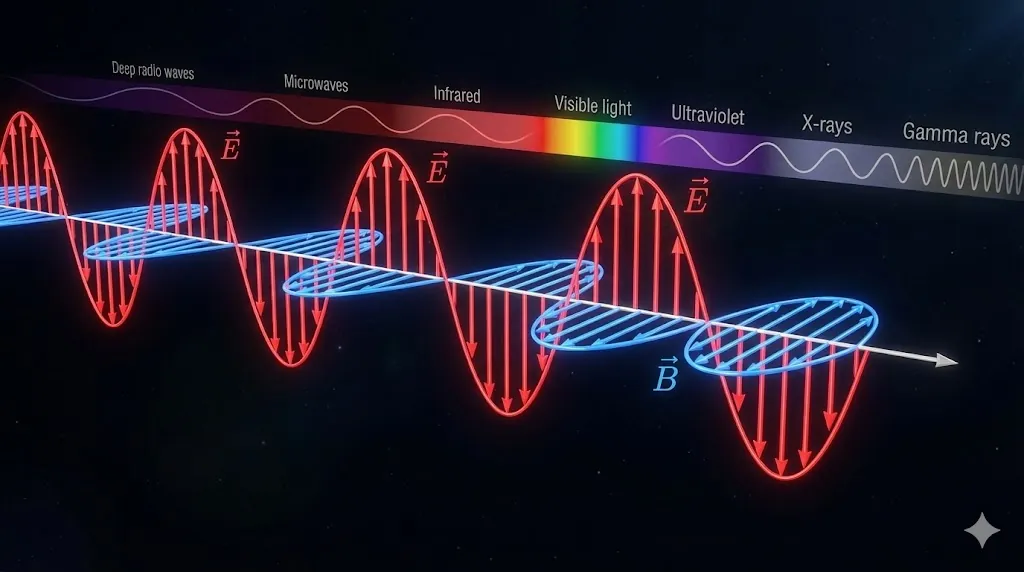
3. Nature of Electromagnetic Waves

Electromagnetic waves are self-sustaining oscillations of electric and magnetic fields in free space. They are transverse in nature.

Graphical representation of E and B fields in an electromagnetic wave. — $\vec{E}$ and $\vec{B}$ oscillate in phase, perpendicular to each other and the direction of wave motion.

Speed of EM Waves (c):

c = \dfrac{1}{\sqrt{\mu_0 \epsilon_0}} \approx 3 \times 10^8 \text{ m/s}

Relation between fields: $c = \dfrac{E_0}{B_0}$

Energy Density:

The energy in EM waves is shared equally between electric and magnetic fields.
$u_{total} = \epsilon_0 E_{rms}^2 = \dfrac{B_{rms}^2}{\mu_0}$

4. The Electromagnetic Spectrum

EM waves are classified by frequency or wavelength. The order from lowest to highest frequency is:

Chart of the electromagnetic spectrum showing frequency ranges and applications.

Type	Wavelength Range	Production & Application
Radio Waves	> 0.1 m	Rapid acceleration of charges in conducting wires. Used in Radio/TV communication.
Microwaves	0.1 m to 1 mm	Klystron/Magnetron valves. Used in Radar, Microwave ovens.
Infrared (IR)	1 mm to 700 nm	Hot bodies, molecular vibrations. Used in Remotes, Physical therapy.
Visible Light	700 nm to 400 nm	Electrons in atoms. It stimulates the human eye.
Ultraviolet (UV)	400 nm to 1 nm	Inner shell electrons, Sun. Used in Water purification, LASIK eye surgery.
X-rays	1 nm to $10^{-3}$ nm	Bombarding metal target with high energy electrons. Used in Medical imaging.
Gamma Rays	< $10^{-3}$ nm	Radioactive decay of nuclei. Used in Cancer treatment.

← Previous: Alternating Current Next: Ray Optics →