CBSE Class 12 › Unit II: Current Electricity

Kirchhoff’s Laws & Circuits

NCERT Chapter 3 (Part 2) • Cells, Networks & Wheatstone Bridge

NCERT 2025–26 Problem Solving Focus

1. Cells, EMF, and Internal Resistance

EMF ( $\epsilon$ ): The potential difference between the positive and negative terminals of a cell when no current flows through it (open circuit).

Internal Resistance ( $r$ ): The finite resistance offered by the electrolyte inside the cell to the flow of current.

Terminal Potential Difference ( $V$ ):

When a current $I$ is drawn from the cell, the potential difference $V$ is less than EMF: $V = \epsilon - I r$ .

2. Derivation: Cells in Series

Consider two cells ( $\epsilon_1, r_1$ ) and ( $\epsilon_2, r_2$ ) connected in series (end-to-end) between points A and C.

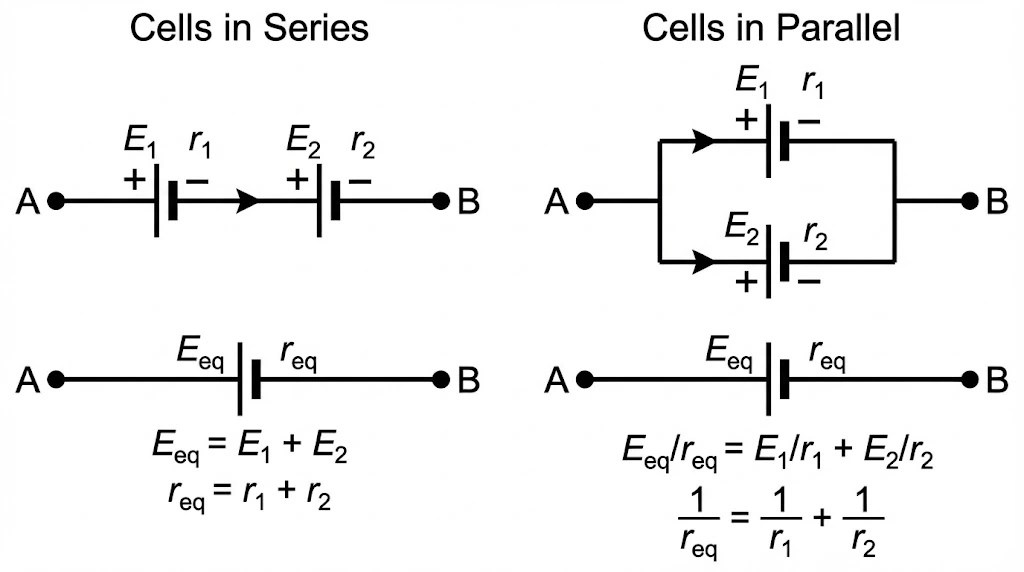
Diagram of cells connected in series showing potentials at points A, B, and C. — Two cells connected in series. The same current I flows through both.

Derivation: Equivalent EMF (Series) 3 Marks

Step 1: Potential Difference across first cell
Let $V(A)$ and $V(B)$ be potentials at the terminals. For the first cell:
$V_{AB} = V(A) - V(B) = \epsilon_1 - I r_1$ .

Step 2: Potential Difference across second cell
Similarly, for the second cell connected between B and C:
$V_{BC} = V(B) - V(C) = \epsilon_2 - I r_2$ .

Step 3: Total Potential Difference
The potential difference across the combination (A to C) is the sum:
$V_{AC} = V_{AB} + V_{BC} = (\epsilon_1 - I r_1) + (\epsilon_2 - I r_2)$
Rearranging terms:
$V_{AC} = (\epsilon_1 + \epsilon_2) - I (r_1 + r_2)$ .

Step 4: Comparison with Equivalent Cell
If we replace the combination with a single cell of $\epsilon_{eq}$ and $r_{eq}$ , the equation would be:
$V_{AC} = \epsilon_{eq} - I r_{eq}$ .
Comparing the coefficients:
$\epsilon_{eq} = \epsilon_1 + \epsilon_2$ and $r_{eq} = r_1 + r_2$ .

3. Derivation: Cells in Parallel

Consider two cells connected in parallel between points $B_1$ and $B_2$ . Currents $I_1$ and $I_2$ flow out of the positive terminals.

Derivation: Equivalent EMF (Parallel) 3 Marks

Step 1: Current Equation
By conservation of charge (junction rule), the main current $I$ splits:
$I = I_1 + I_2$ .

Step 2: Voltage Equations
Since they are in parallel, the terminal voltage $V$ is the same for both cells.
For cell 1: $V = \epsilon_1 - I_1 r_1 \Rightarrow I_1 = \frac{\epsilon_1 - V}{r_1}$ .
For cell 2: $V = \epsilon_2 - I_2 r_2 \Rightarrow I_2 = \frac{\epsilon_2 - V}{r_2}$ .

Step 3: Substitute into Sum
Substitute $I_1$ and $I_2$ into the current equation:
$I = \left(\frac{\epsilon_1 - V}{r_1}\right) + \left(\frac{\epsilon_2 - V}{r_2}\right) = \left(\frac{\epsilon_1}{r_1} + \frac{\epsilon_2}{r_2}\right) - V\left(\frac{1}{r_1} + \frac{1}{r_2}\right)$ .

Step 4: Rearrange for V
Multiplying by $r_1 r_2$ and rearranging to isolate $V$ :
$V = \frac{\epsilon_1 r_2 + \epsilon_2 r_1}{r_1 + r_2} - I \left(\frac{r_1 r_2}{r_1 + r_2}\right)$ .

Step 5: Final Result
Comparing this with the standard equation $V = \epsilon_{eq} - I r_{eq}$ , we get:
$\epsilon_{eq} = \frac{\epsilon_1 r_2 + \epsilon_2 r_1}{r_1 + r_2}$ and $r_{eq} = \frac{r_1 r_2}{r_1 + r_2}$ .

4. Kirchhoff’s Rules

For complex circuits where Ohm’s law isn’t sufficient, we use Kirchhoff’s Rules.

1. Junction Rule (Charge Conservation)
At any junction, the sum of currents entering equals the sum of currents leaving.
$\sum I_{in} = \sum I_{out}$ .

2. Loop Rule (Energy Conservation)
The algebraic sum of changes in potential around any closed loop is zero.
$\sum \Delta V = 0$ .

5. Solved Example: Kirchhoff’s Rules

Let’s apply Kirchhoff’s rules to solve a typical circuit problem (Based on NCERT Example 3.6).

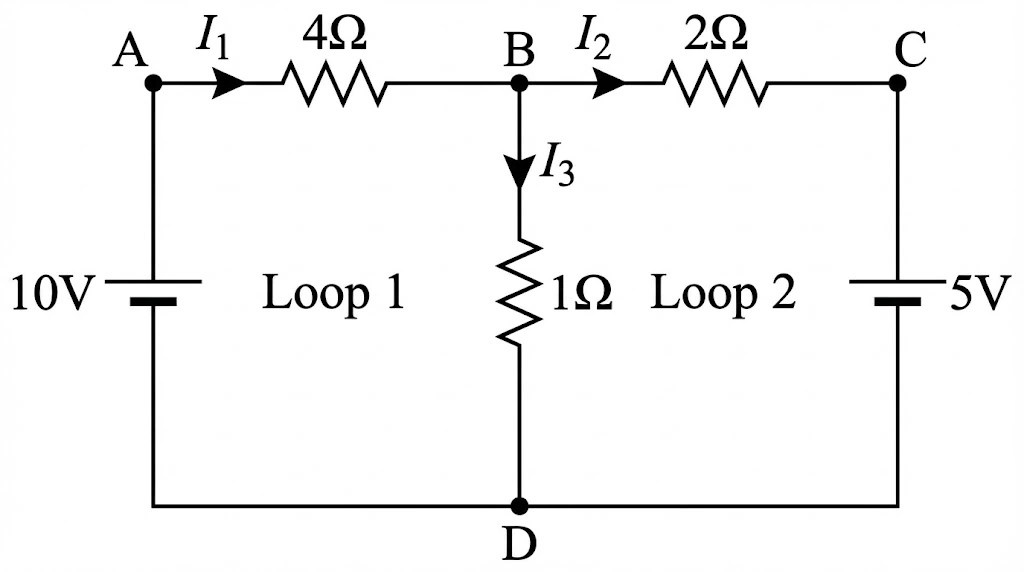
Circuit diagram showing a multi-loop network with 10V and 5V batteries and resistors. — Network to determine currents in each branch using Mesh Analysis.

Objective:

Find currents $I_1$ , $I_2$ , and $I_3$ in the circuit where resistors are $4\Omega, 2\Omega, 1\Omega$ and batteries are $10V, 5V$ .

Solution: Applying the Rules Example Problem

Step 1: Apply Junction Rule at Node B
Current entering = current leaving:
$I_1 = I_2 + I_3$ → Equation (1)

Step 2: Apply Loop Rule to Loop 1 (ABDA — Left Loop with 10V)
Start at A, go clockwise: through 10V battery → 4Ω → 1Ω → back to A.
– Voltage rise: +10V (battery)
– Voltage drop: $4I_1$ (across 4Ω, with current)
– Voltage drop: $I_3$ (across 1Ω, since $I_3$ flows downward, same as loop direction)
So: $+10 - 4I_1 - I_3 = 0$ → $4I_1 + I_3 = 10$ → Equation (2)

Step 3: Apply Loop Rule to Loop 2 (BCDB — Right Loop with 5V)
Start at B, go clockwise: through 2Ω → 5V battery → 1Ω → back to B.
– Voltage drop across 2Ω: $2I_2$ (current $I_2$ is in direction of loop) → $-2I_2$
– Voltage drop across 5V battery: going from **+ to –** → voltage drop → $-5$
– Voltage across 1Ω: we’re going **upward**, against $I_3$ → this is a **voltage rise** → $+I_3$
So: $-2I_2 - 5 + I_3 = 0$ → $-2I_2 + I_3 = 5$ → Equation (3)

Step 4: Solve the System of Equations
From Equation (1): $I_1 = I_2 + I_3$ → Substitute into Equation (2):
$4(I_2 + I_3) + I_3 = 10$ → $4I_2 + 4I_3 + I_3 = 10$ → $4I_2 + 5I_3 = 10$ → Equation (4)
Now use Equation (3): $-2I_2 + I_3 = 5$ → Multiply by 2: $-4I_2 + 2I_3 = 10$ → Equation (5)
Add Equation (4) and Equation (5):
$(4I_2 + 5I_3) + (-4I_2 + 2I_3) = 10 + 10$ → $7I_3 = 20$ → $I_3 = \frac{20}{7} \approx 2.857\,A$
Plug into Equation (3): $-2I_2 + \frac{20}{7} = 5$ → $-2I_2 = 5 - \frac{20}{7} = \frac{35 - 20}{7} = \frac{15}{7}$ → $I_2 = -\frac{15}{14} \approx -1.071\,A$
Plug into Equation (1): $I_1 = I_2 + I_3 = -\frac{15}{14} + \frac{20}{7} = -\frac{15}{14} + \frac{40}{14} = \frac{25}{14} \approx 1.786\,A$

Final Answer:
$\boxed{I_1 = \dfrac{25}{14}\,A \approx 1.786\,A},\quad \boxed{I_2 = -\dfrac{15}{14}\,A \approx -1.071\,A},\quad \boxed{I_3 = \dfrac{20}{7}\,A \approx 2.857\,A}$

Interpretation: The negative sign for $I_2$ means the actual direction of current $I_2$ is **opposite** to what was assumed (i.e., from C to B, not B to C). This is physically possible and common in circuit analysis. The 1Ω branch carries significant current ( $I_3$ ) because the 5V battery “pushes” against the 10V side, creating a potential difference that drives current through the middle branch.

6. Wheatstone Bridge

An arrangement of four resistors used to measure an unknown resistance accurately. It consists of four arms (R1, R2, R3, R4) and a galvanometer.

Wheatstone bridge circuit diagram showing four arms and a galvanometer. — Balanced Condition: No current through Galvanometer ( $I_g = 0$ ).

Derivation: Balanced Condition 3 Marks

Step 1: Loop Rule (Left Loop)
Apply loop rule to ADBA (assuming $I_g = 0$ ): $-I_1 R_1 + I_2 R_2 = 0 \Rightarrow I_1 R_1 = I_2 R_2$ .

Step 2: Loop Rule (Right Loop)
Apply loop rule to CBDC: $I_2 R_4 - I_1 R_3 = 0 \Rightarrow I_1 R_3 = I_2 R_4$ .

Step 3: Final Relation
Dividing the two equations: $\frac{R_2}{R_1} = \frac{R_4}{R_3}$ .

← Previous: Current & Ohm’s Law Next Unit: Moving Charges →