by Introduction
Gauss’s Law for magnetism stands as a cornerstone in the study of magnetism and the broader field of electromagnetism. Magnetism involves the behavior of magnetic fields and forces, which originate from electric currents or magnetic materials. This law encapsulates a powerful insight: it states that the net magnetic flux through any closed surface equals zero. Understanding this fundamental principle provides a deeper appreciation of how magnetic field lines operate and why there are no isolated magnetic poles.
This guide explores Gauss’s Law for magnetism in detail by examining its theoretical background, connections to Maxwell’s equations, and practical implications. The following sections offer step-by-step explanations that incorporate both short-tail and long-tail keywords, making the content accessible and search-friendly.
What Is Gauss’s Law for Magnetism?
Gauss’s Law for magnetism can be expressed mathematically using the equation:
![\[\nabla \cdot \mathbf{B} = 0\]](https://physicsqanda.com/wp-content/ql-cache/quicklatex.com-cc50e46869a6d2d4748a73b5f52b904c_l3.png "Rendered by QuickLaTeX.com")
where 
represents the magnetic field. Alternatively, in integral form, it is written as:
![\[\oint_S \mathbf{B} \cdot d\mathbf{A} = 0\]](https://physicsqanda.com/wp-content/ql-cache/quicklatex.com-5b774bb40f8f43f197eb1ce61f3a5f20_l3.png "Rendered by QuickLaTeX.com")
where (\mathbf{B}) represents the magnetic field. Alternatively, in integral form, it is written as:
![\[\oint_S \mathbf{B} \cdot d\mathbf{A} = 0\]](https://physicsqanda.com/wp-content/ql-cache/quicklatex.com-074dcae496faba9fc713076d10033c3f_l3.png "Rendered by QuickLaTeX.com")
These equations highlight that the total magnetic flux passing out of a closed surface 
sums to zero. In other words, as much magnetic field flows into the enclosed volume as flows out. This property reinforces the notion that magnetic monopoles (isolated north or south poles) do not exist in nature.
Key Points:
- No isolated poles: Unlike electric charges, which exist independently as positive or negative, magnetic poles always come in north–south pairs.
- Consistent flux balance: Magnetic field lines form continuous loops, ensuring that the net flux around a closed surface remains balanced.
Connection to Maxwell’s Equations
Gauss’s Law for magnetism is one of the four Maxwell’s equations, the fundamental set of equations that govern classical electromagnetism. These equations are:
- Gauss’s Law for Electricity
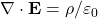
- Gauss’s Law for Magnetism
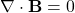
- Faraday’s Law of Induction
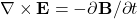
- Ampère’s Law (with Maxwell’s correction)
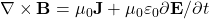
While Gauss’s Law for magnetism is among the simplest in appearance, it carries profound implications for understanding electromagnetic fields, their interactions, and the concept of magnetic flux.
Core Concepts and Terminology
- Magnetic Field
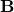
- Describes the magnetic influence at each point in space.
- Characterized by both magnitude and direction, making it a vector field.
- Magnetic Flux
- Defined as
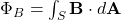, where 
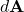is a vector representing the infinitesimal area on a surface 
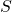. - Represents the total “flow” of the magnetic field through a surface.
- Defined as
- Closed Surface
- A surface that completely encloses a volume without boundaries. Examples include spheres, cubes, or any closed geometry.
- The integral form of Gauss’s Law for magnetism considers the net flux through such a closed surface.
- Magnetic Monopole
- A hypothetical particle with only a north or a south magnetic pole.
- Current understanding and experiments suggest no evidence of their existence, which aligns with .
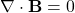You may also want to Why Do Magnets Lose Their Magnetism Over Time?
Physical Interpretation of Gauss’s Law for Magnetism
- Continuous Looping of Field Lines
- Magnetic field lines always form closed loops or extend to infinity.
- There is no net “start” or “end” to these lines, unlike electric field lines that begin or end on charges.
- Implication for Real-World Magnetic Systems
- When analyzing devices such as solenoids, transformers, or electromagnets, Gauss’s Law provides essential insights into how magnetic fields distribute themselves.
- Each region of a device has an equal amount of magnetic flux entering and exiting, confirming that no section serves as an isolated source of the field.
- Symmetry and Simplification in Problems
- Certain symmetrical configurations of magnetic fields, such as cylindrical or spherical shapes, make it easier to apply Gauss’s Law directly.
- Even when direct application is not straightforward, the concept of net zero flux informs boundary conditions and system constraints.
Practical Applications of Gauss’s Law for Magnetism
- Magnetic Storage Devices
- Hard disk drives and magnetic tape rely on stable, looped magnetic fields to record and retrieve data.
- Knowledge of how flux lines behave ensures data integrity and device reliability.
- Electric Motor and Generator Design
- Understanding magnetic fields in rotating machinery helps improve efficiency and performance.
- Gauss’s Law ensures accurate calculations of flux distribution within stators and rotors.
- Magnetohydrodynamics (MHD)
- Studies the behavior of conductive fluids (e.g., plasma in fusion reactors).
- The net-zero flux principle is essential for containment fields, cooling systems, and the overall stability of plasma configurations.
- Diagnostic Tools in Research
- Techniques like Magnetic Resonance Imaging (MRI) capitalize on uniform magnetic fields to produce accurate scans.
- Gauss’s Law for magnetism helps inform the design of the coils and magnets that maintain these fields without stray sources or sinks.
Tips for Further Study
- Explore Mathematical Techniques: Delve into vector calculus, focusing on surface integrals and divergence operations to gain a deeper mathematical perspective on magnetism.
- Examine Related Equations: Compare Gauss’s Law for magnetism to the other Maxwell’s equations for a holistic view of electromagnetism.
- Look Into Advanced Research: Investigate current experiments searching for magnetic monopoles. Although none have been found yet, these pursuits push the boundaries of knowledge in modern physics.
Conclusion
Gauss’s Law for magnetism underscores the balanced, continuous nature of magnetic fields and constitutes a vital segment of Maxwell’s equations. This law not only shapes fundamental physics but also informs everyday technologies, from advanced data storage to medical imaging.
For more in-depth exploration, consult reputable academic sources such as MIT’s OpenCourseWare on Electromagnetism or refer to internal pages featuring additional insights on magnetic fields and Maxwell’s equations. Subscribing to educational newsletters or checking advanced physics forums can also offer regular updates on emerging research related to magnetic monopoles and novel applications.
