CBSE Class 12 › Unit II: Current Electricity

Current Electricity (Basics)

NCERT Chapter 3 (Part 1) • Ohm’s Law, Drift Velocity & Power

NCERT 2025–26 Derivations Included

1. Electric Current

Charges in motion constitute an electric current. In a conductor, if a net charge $\Delta Q$ flows across a cross-section in time $\Delta t$ , the average current is defined as $I = \Delta Q / \Delta t$ .

I(t) = \lim_{\Delta t \to 0} \frac{\Delta Q}{\Delta t} = \frac{dq}{dt}

SI Unit: Ampere (A)

2. Ohm’s Law

For a conductor, the potential difference $V$ across its ends is directly proportional to the current $I$ flowing through it, provided physical conditions (like temperature) remain constant.

V = I R

The constant $R$ is the Resistance. It depends on the dimensions of the conductor:

Proportional to length $l$ .
Inversely proportional to area $A$ .

Thus, $R = \rho \frac{l}{A}$ , where $\rho$ is Resistivity.

3. Drift of Electrons & Resistivity

In a metal, electrons move randomly with high thermal speeds. The average velocity is zero. When an electric field $E$ is applied, electrons experience a force $-eE$ and accelerate, acquiring a small net velocity opposite to the field called Drift Velocity ( $v_d$ ).

Diagram comparing random thermal motion and drift velocity path. — Drift velocity is a small bias superposed on chaotic thermal motion.

Derivation: Drift Velocity 3 Marks

Step 1: Acceleration
Force on electron $F = -eE$ . Acceleration $a = -eE/m$ .

Step 2: Relaxation Time
Electrons collide with ions. Let $\tau$ be the average time between successive collisions (relaxation time). The average velocity gained is: $v_d = a\tau = -\frac{eE}{m}\tau$ .

Step 3: Current Relation
Volume of conductor = $A \times (v_d \Delta t)$ . Total charge $\Delta Q = n e A v_d \Delta t$ .
Current $I = \Delta Q / \Delta t = n e A v_d$ .

Step 4: Vector Form
Current density $j = I/A$ . Thus, $\vec{j} = \frac{ne^2\tau}{m}\vec{E}$ . Comparing with Ohm’s Law ( $j = \sigma E$ ), we get conductivity: $\sigma = \frac{ne^2\tau}{m}$ .

4. Temperature Dependence

Resistivity $\rho = 1/\sigma = \frac{m}{ne^2\tau}$ . It depends on temperature:

Metals: $\tau$ decreases as temperature rises (more collisions). So, $\rho$ increases.
Semiconductors: $n$ increases significantly with temperature. So, $\rho$ decreases.

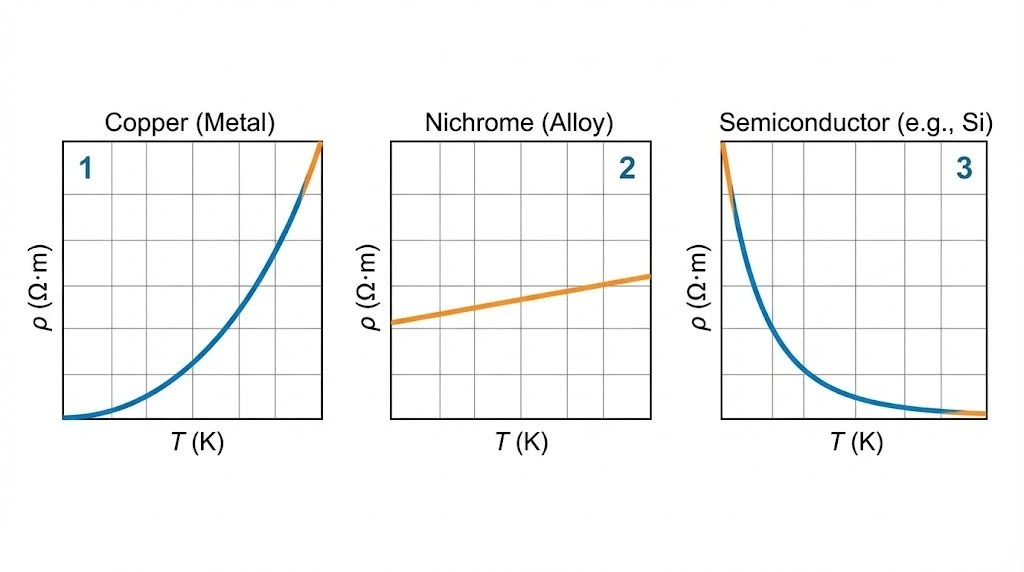
Graphs of resistivity vs temperature for Copper, Nichrome, and Semiconductor. — (a) Copper (non-linear), (b) Nichrome (linear), (c) Semiconductor (inverse).

Formula:

For metals over a limited range: $\rho_T = \rho_0 [1 + \alpha(T - T_0)]$ .

5. Electrical Energy & Power

The energy dissipated as heat in a conductor is the work done to move charges against resistance.

P = V I = I^2 R = \frac{V^2}{R}

← Previous Chapter Next: Kirchhoff’s Laws →