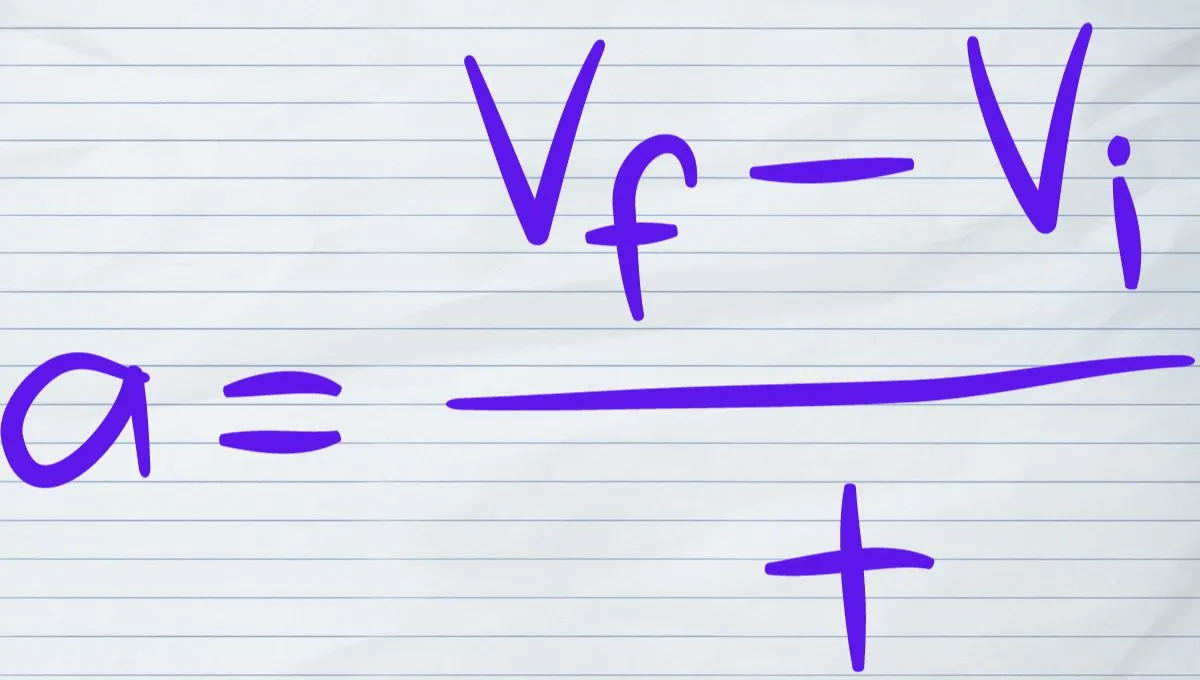How To Find Acceleration

Spread the love

Understanding and Calculating Acceleration

Acceleration is a fundamental concept in physics, describing how quickly an object’s speed or direction changes. It’s not just about speed; it’s about how that speed changes over time. This post will guide you through understanding and calculating acceleration in different scenarios.

Contents hide

1 What is Acceleration?

2 Types of Accelerations

3 Step-by-Step Guide to Calculate Acceleration

3.1 Example Problem

4 Calculating Acceleration Using Force and Mass

4.1 Example

5 Calculating Centripetal Acceleration

5.1 Example

6 Some important points:

7 Problems:

8 Acceleration Calculator

8.1 1) Acceleration (Initial & Final Velocity, Time Interval)

8.2 2) Acceleration (Force, Mass)

8.3 3) Centripetal Acceleration (Speed, Radius)

What is Acceleration?

Acceleration is a measure of the rate at which an object’s velocity changes.

It can be a speed up, a slow down (deceleration), or a change in direction.

It is a vector quantity, which means it has both magnitude (how much) and direction (which way).

Definition: The time rate of change of velocity is called acceleration.

$\boxed{\bf{Acceleration = \dfrac{\text{Change in velocity}}{\text{Time interval}}}}$

Unit: SI unit is $m/s^2$ , CGS unit is $cm/s^2$

Dimensions: $[LT^{-2}]$

Types of Accelerations

Uniform Acceleration: If velocity changes by equal amounts in equal intervals of time.

Non-uniform(variable) acceleration: If velocity changes by unequal amounts in equal intervals of time.

verage acceleration: It is the ratio of total change in velocity to the total time taken.

$\vec{a}_{avg} = \dfrac{\Delta \vec{v}}{\Delta t} = \dfrac{\vec{v_2} - \vec{v_1}}{t_2-t_1}$

Instantaneous acceleration: The acceleration of an object at a given instant of time.

$\vec{a}_{inst} = \underset{\Delta t \to 0}{Lim}\dfrac{\Delta \vec{v}}{\Delta t}=\dfrac{d\vec{v}}{dt}$

$\vec{a}_{inst} = \dfrac{d}{dt}\left(\dfrac{d\vec{s}}{dt}\right) = \dfrac{d^2\vec{s}}{dt^2}$

Using equation of motion: To calculate the acceleration we can use the equations of motion.

$v = u + at, s = ut + \frac{1}{2}at^2$ and $v^2 = u^2 +2as$

Here, $u$ = initial velocity, $v$ = final velocity, $t$ = time interval and $a$ = acceleration.

Force and mass: When a system is given in which many forces are acting, like the system of connected bodies. To get the acceleration we can use the formula.

$\boxed{\rm acceleration = \dfrac{\text{Net deriving force}}{\text{total mass}}}$

Centripetal Acceleration: This is the acceleration experienced by an object moving in a circular path, directed towards the center of the circle.

The formula for centripetal acceleration is either $a_c = \dfrac{v^2}{r}$ , where $v$ is the speed of the object, and $r$ is the radius of the circular path, or $a_c=\omega^2 r$ , where $\omega$ is the angular velocity.

The basic formula to calculate acceleration ( $\vec{a}$ ) is:

$\vec{a} = \dfrac{\Delta\vec{ v}}{\Delta t}$

Where:

$\Delta v$ is the change in velocity

$\Delta t$ is the time over which the change occurs

Step-by-Step Guide to Calculate Acceleration

Identify the Initial and Final Velocities:

Determine the starting velocity ( $v_i$ ) and the final velocity ( $v_f$ ) of the object.

Calculate the Change in Velocity:

Subtract the initial velocity from the final velocity. $\Delta v = v_f - v_i$ .

Determine the Time Interval:

Find out how much time ( $\Delta t$ ) it took for this change in velocity to happen.

Apply the Formula:

Plug these values into the acceleration formula.

Example Problem

Let’s say a car speeds up from 0 to 60 km/h in 5 seconds. What is its acceleration?

Initial velocity, $v_i = 0$ km/h

Final velocity, $v_f = 60$ km/h

Time interval, $\Delta t = 5$ seconds

Change in velocity, $\Delta v = 60 - 0 = 60$ km/h

Convert km/h to m/s: $\rm 60 km/h = 60\times\dfrac{5}{18} m/s= 16.67 m/s$

Apply the formula: $a = \dfrac{16.67\, \text{m/s}}{5\, \text{s}} = 3.33\, \text{m/s}^2$

Calculating Acceleration Using Force and Mass

Understand Newton’s Second Law of Motion: Newton’s Second Law states that the force acting on an object is equal to the mass of that object times its acceleration. It is usually written as $F = ma$ .

Identify the Force ( $F$ ): Determine the net force acting on the object. This is the sum of all the forces acting on the object. Make sure to use the same unit of force throughout your calculation, typically Newtons (N).

Determine the Mass ( $m$ ): Find the mass of the object. Again, ensure consistency in units, typically kilograms (kg).

Rearrange the Equation: Since $F = ma$ , to find acceleration ( $a$ ), rearrange the equation to $a = \frac{F}{m}$ .

Plug in the Values: Substitute the values of $F$ and $m$ into the equation.

Calculate the Acceleration: Perform the division to find the acceleration. The unit of acceleration is meters per second squared ( $m/s^2$ ).

Interpret the Result: Understand the direction and magnitude of the acceleration as it relates to the problem.

Example

Problem Statement:
Suppose a force of 10 Newtons is applied to a mass of 2 kilograms. What is the acceleration of the mass?

Solution Steps:

Identify Force ( $F$ ) and Mass ( $m$ ):

Force, $F = 10 \, \text{Newtons}$
Mass, $m = 2 \, \text{kilograms}$

Use Newton’s Second Law ( $F = ma$ ):

Acceleration, $a = \frac{F}{m}$

Substitute the Values:

$a = \frac{10 \, \text{N}}{2 \, \text{kg}}$

Calculate Acceleration:

$a = 5 \, \text{m/s}^2$

Answer:
The acceleration of the mass is $5 \, \text{m/s}^2$ .

Calculating Centripetal Acceleration

Understand Centripetal Acceleration: Centripetal acceleration is the acceleration experienced by an object moving in a circular path, directed towards the center of the circle.

Identify the Velocity ( $v$ ) or Speed: Determine the constant speed of the object moving in the circular path. The speed should be in meters per second ( $m/s$ ).

Determine the Radius of the Circle ( $r$ ): Find the radius of the circular path. This should be in meters (m).

Use the Centripetal Acceleration Formula: The formula for centripetal acceleration ( $a_c$ ) is $a_c = \frac{v^2}{r}$ , where $v$ is the velocity and $r$ is the radius.

Plug in the Values: Substitute the values of $v$ and $r$ into the equation.

Calculate the Centripetal Acceleration: Perform the calculation by squaring the velocity and dividing it by the radius.

Interpret the Result: The resulting centripetal acceleration, in meters per second squared ( $m/s^2$ ), indicates how much and how quickly the velocity of the object is changing direction.

Example

Problem Statement:
A car is moving at a constant speed of 20 meters per second around a circular track with a radius of 50 meters. What is the car’s centripetal acceleration?

Solution Steps:

Identify Velocity ( $v$ ) and Radius ( $r$ ):

Velocity, $v = 20 \, \text{m/s}$
Radius, $r = 50 \, \text{meters}$

Use the Centripetal Acceleration Formula ( $a_c = \frac{v^2}{r})$ :

Substitute the Values:

$a_c = \frac{(20 \, \text{m/s})^2}{50 \, \text{m}}$

Calculate Centripetal Acceleration:

$a_c = \frac{400 \, \text{m}^2/\text{s}^2}{50 \, \text{m}}$
$a_c = 8 \, \text{m/s}^2$

Answer:
The car’s centripetal acceleration is $8 \, \text{m/s}^2$ .

Some important points:

If acceleration is zero, then motion will be uniform.
If acceleration is constant, then motion will be non-uniform.
If velocity is given as a function of position, then $a = v\dfrac{dv}{ds}$
Acceleration is the slope of velocity versus time graph.
A particle on the highest point of its trajectory has zero vertical velocity but non-zero acceleration.

Problems:

(1) Mr. Smith applies constant deceleration to his vehicle, reducing the speed from 35 m/s to 25 m/s across a span of 300 meters. (a) Determine the duration of this deceleration period. (b) Calculate the rate of deceleration. (c) Assuming Mr. Smith maintains this constant deceleration, estimate the additional time required for the vehicle to come to a complete stop and the extra distance it would traverse during this time.

[(a) $10 s$ , (b) $-1 m/s^2$ , (c) $35s$ , $312.5 m$ ]

(2) A 100 m long train accelerates uniformly from rest. If the front of the train passes a railway worker 25 m away from the station at a speed of 15 m/s, what will be the speed of the back part of the train as it passes the worker?

Train accelerates from rest for first 25 m to reach the worker with a speed of 15m/s

Apply the equation, $v^2 - u^2 = 2as$

$15^2 - 0^2 = 2a(25) ---- (1)$

Now, when train passes the worker, the total distance covered by the engine is 125m(=25 m + 100 m)

$v^2 - 0^2 = 2a(125) ----(2)$

Divide equation (2) by (1)

$\dfrac{v^2}{15^2} =\dfrac{125}{25}$

$v^2 = 15^2\times 5$

$v = 15\sqrt{5} m/s = 33.54 m/s$

Acceleration Calculator

1) Acceleration (Initial & Final Velocity, Time Interval)

Initial Velocity (m/s):
Final Velocity (m/s):
Time Interval (s):

Acceleration: m/s²

2) Acceleration (Force, Mass)

Force (N):
Mass (kg):

Acceleration: m/s²

3) Centripetal Acceleration (Speed, Radius)

Speed (m/s):
Radius (m):

Centripetal Acceleration: m/s²

What is Acceleration?

Types of Accelerations

Step-by-Step Guide to Calculate Acceleration

Example Problem

Calculating Acceleration Using Force and Mass

Example

Calculating Centripetal Acceleration

Example

Some important points:

Problems:

Acceleration Calculator

1) Acceleration (Initial & Final Velocity, Time Interval)

2) Acceleration (Force, Mass)

3) Centripetal Acceleration (Speed, Radius)

admin

Leave a Reply Cancel reply

What is Acceleration?

Types of Accelerations

Step-by-Step Guide to Calculate Acceleration

Example Problem

Calculating Acceleration Using Force and Mass

Example

Calculating Centripetal Acceleration

Example

Some important points:

Problems:

Acceleration Calculator

1) Acceleration (Initial & Final Velocity, Time Interval)

2) Acceleration (Force, Mass)

3) Centripetal Acceleration (Speed, Radius)

admin

You might also like

Fluid Mechanics: Definition, Theory, Equations, and Applications of Fluids

Why Do Magnets Lose Their Magnetism Over Time?

Light Year: Measurement of Cosmic Distances

Leave a Reply Cancel reply