Consider a particle of mass m moving in one dimension under a force with the potential U(x) = k(2x^3 − 5x^2 + 4x)...

Spread the love

Consider a particle of mass m moving in one dimension under a force with the
potential $U(x) = k(2x^3 − 5x^2 + 4x)$ , where the constant $k > 0$ . Show that
the point $x = 1$ corresponds to a stable equilibrium position of the particle.

Answer:

To determine the stability of equilibrium at a point, we will analyze the force acting on the particle and investigate the curvature of the potential energy function at that point.

Contents hide

1 Step 1: Determine the force acting on the particle

2 Step 2: Determine the equilibrium conditions Do

3 Step 3: Find the values of

4 Step 4: At Determine the nature of the equilibrium

5 Additional analysis: equilibrium at

6 Conclusion

Step 1: Determine the force acting on the particle

The force $F(x)$ acting on the particle is equal to the negative derivative of the potential energy $U(x)$ :

$F(x) = -\frac{dU}{dx}$

First, find the derivative of $U(x)$ :

$\begin{align<em>} U(x) &= k(2x^3 - 5x^2 + 4x) \ \frac{dU}{dx} &= k\left(6x^2 - 10x + 4\right) \end{align</em>}$

Therefore, the force is:

$F(x) = -\frac{dU}{dx} = -k\left(6x^2 - 10x + 4\right)$

Step 2: Determine the equilibrium conditions Do

At equilibrium, the total force on the particle is zero:

$F(x) = 0 \implies -k\left(6x^2 - 10x + 4\right) = 0$

Since $k > 0$ , we can simplify the equation:

$6x^2 - 10x + 4 = 0$

Simplify the equation by dividing it by 2:

$3x^2 - 5x + 2 = 0$

Step 3: Find the values of 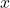$x$

Use the formula for a quadratic equation:

$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$

Where for $3x^2 - 5x + 2 = 0$ :

$a = 3$
$b = -5$
$c = 2$

Calculate the discriminant:

$\Delta = b^2 - 4ac = (-5)^2 - 4(3)(2) = 25 - 24 = 1$

Now calculate the values:

$\begin{align<em>} x &= \frac{-(-5) \pm \sqrt{1}}{2 \times 3} \ &= \frac{5 \pm 1}{6} \end{align</em>}$

This gives the equilibrium conditions:

$x = \frac{5 + 1}{6} = 1$
$x = \frac{5 - 1}{6} = \frac{4}{6} = \frac{2}{3}$

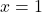Step 4: At $x = 1$ Determine the nature of the equilibrium

To check stability at $x = 1$ , evaluate the second derivative of the potential energy function:

$\frac{d^2U}{dx^2} = k\left(12x - 10\right)$

At $x = 1$ , evaluate:

$\frac{d^2U}{dx^2}\Big|_{x=1} = k(12 \times 1 - 10) = k(2)$

Since $k > 0$ , therefore:

$\frac{d^2U}{dx^2}\Big|_{x=1} > 0$

The positive second derivative indicates that the potential energy function has a local minimum at $x = 1$ . Therefore, at this point the particle is in a stable equilibrium.

Additional analysis: equilibrium at 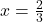$x = \frac{2}{3}$

For completeness, analyze stability at $x = \frac{2}{3}$ :

$\frac{d^2U}{dx^2}\Big|_{x=\frac{2}{3}} = k\left(12 \times \frac{2}{3} - 10\right) = k(8 - 10) = -2k$

Since $k > 0$ , therefore:

$\frac{d^2U}{dx^2}\Big|_{x=\frac{2}{3}} < 0$

The negative second derivative indicates that the potential energy has a local maximum at $x = \frac{2}{3}$ , indicating an unstable equilibrium.

Conclusion

By analyzing the potential energy function and its differentials, we have shown that:

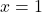$x = 1$ is a stable equilibrium position (local minimum of $U(x)$ ).
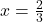$x = \frac{2}{3}$ is an unstable equilibrium position (local maximum of ( U(x) )).

Understanding Stability through Potential Energy

Stable equilibrium occurs when the potential energy is minimum, since small displacements generate restoring forces that push the particle back towards the equilibrium position. In contrast, at the maximum of potential energy, any small displacement moves the particle away from equilibrium, which characterizes unstable equilibrium.

References:

The relationship between potential energy and stability is discussed in textbooks of classical mechanics.
In differential calculus, the second differential test is used to determine the minimum and maximum.

Note: This analysis assumes that $k$ is a positive constant, which affects the sign of the curvature of the force and potential energy functions.

Consider a particle of mass m moving in one dimension under a force with the potential U(x) = k(2x^3 − 5x^2 + 4x)…

Step 1: Determine the force acting on the particle

Step 2: Determine the equilibrium conditions Do

Step 3: Find the values of $x$

Step 4: At $x = 1$ Determine the nature of the equilibrium

Additional analysis: equilibrium at $x = \frac{2}{3}$

Conclusion

Leave a Comment Cancel Reply

Step 1: Determine the force acting on the particle

Step 2: Determine the equilibrium conditions Do

Step 3: Find the values ​​of

Step 4: At Determine the nature of the equilibrium

Additional analysis: equilibrium at

Conclusion

Related Posts

Leave a Comment Cancel Reply

Step 3: Find the values of $x$

Step 4: At $x = 1$ Determine the nature of the equilibrium

Additional analysis: equilibrium at $x = \frac{2}{3}$