Problem:
Show that the electric potential a distance z above the centre of a horizontal circular loop of radius R, which carries a uniform charge density per unit length λ, is given by
![]()
Explanation:
The electric potential at ![]() is derived using the principle of superposition, summing contributions from all infinitesimal elements of the charged circular loop. The electrostatic field strength
is derived using the principle of superposition, summing contributions from all infinitesimal elements of the charged circular loop. The electrostatic field strength ![]() is then obtained as the negative gradient of the potential
is then obtained as the negative gradient of the potential ![]() along the
along the ![]() -axis.
-axis.
For a uniform charge distribution on a circular loop:
- Compute ( V ) using the distance formula
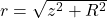 .
. - Differentiate
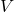 with respect to
with respect to  to get
to get 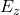 .
.
Solution:
- Electric Potential
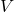 :
:
The total charge on the loop is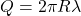 .
.
At a distance above the center of the loop, the electric potential is given by:
above the center of the loop, the electric potential is given by:![Rendered by QuickLaTeX.com \[V = \frac{1}{4\pi \epsilon_0} \int \frac{\lambda \, dl}{r}\]](https://physicsqanda.com/wp-content/ql-cache/quicklatex.com-230f906a6c00283d1d2d58c720b412b2_l3.png)
For a uniform loop,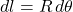 , and
, and 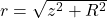 (constant for all points on the loop).
(constant for all points on the loop).
Substituting:
![]()
The integral simplifies as ![]() is constant:
is constant:
![]()
![]()
![]()
This matches the given expression for ![]() .
.
- Electric Field
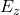 :
:
The field strength along the -axis is obtained from the derivative of
-axis is obtained from the derivative of 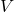 :
:![Rendered by QuickLaTeX.com \[E_z = -\frac{\partial V}{\partial z}\]](https://physicsqanda.com/wp-content/ql-cache/quicklatex.com-3eb5bb82daf4c2353266d86b46c86789_l3.png)
Substitute ![]() :
:
![]()
![]()
Using the chain rule:
![]()
Substitute back:
![]()
![]()
Final Answer:
The electric potential is:
![]()
The electric field strength along the ( z )-axis is:
![]()