Equations of motion
Equations of motion are very helpful in finding the velocity, position, and acceleration at a particular time for a particle. These equations are applicable to vectors only. You always get displacement, not distance but in one-dimensional motion, if the particle is not reversing its direction then only the distance and displacement are the same otherwise distance is more than the displacement. You will get velocity not speed but in one-dimensional motion, there is only one direction so speed and velocity are the same.
There are five equations of motion, these equations are applicable to constant acceleration only.
![]()
![]()
![]()
![]()
![]()
Derivation of First Equation of motion
The first equation of motion contains four variables initial velocity(u), acceleration(a), time(t), and final velocity(v). With help of the first equation of motion, final velocity can be calculated using the values of initial velocity, acceleration, and the given time.
The rate of change of velocity is acceleration, therefore
![]()
![]()
Integrating both the sides
![]()
![]()
![]()
![]()
Derivation of Second Equation of motion
The rate of change of displacement is the velocity, therefore
![]()
![]()
From the first equation of motion, we have
![]()
![]()
Integrating both the sides
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed { \boxed{s= ut+ \frac {1}{2} a t^2}}\]](https://physicsqanda.com/wp-content/ql-cache/quicklatex.com-fe4bfd0be1f0d172bf22a19cefbedc5e_l3.png)
Derivation of Third Equation of motion
Again we have to use definition formula of acceleration. That is :
![]()
Multiply both the side by ds.
![]()
![]()
![]()
Integrating both the sides.
![]()
![]()
![]()
![]()
![]()
Derivation of Fourth Equation of motion
From the second equation of motion we have
![]()
Substituting the value of (u) from the first equation of motion,
![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{\boxed{s=vt-\frac{1}{2}at^2}}\]](https://physicsqanda.com/wp-content/ql-cache/quicklatex.com-30e2b475a9c33ad4a3dba28a3fbf8894_l3.png)
Read More: Measurement
Derivation of Fifth Equation of motion
This equation is about the distance traveled by a body in the (n^{th}) second.
The distance traveled by the body in the first (n) seconds is given by the equation
![]()
The distance traveled by the body in the first (n-1) seconds is given by the equation
![]()
To get the distance traveled by the body in the (n^2) second, subtract the equation ((2)) from the equation ((1))
![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{\boxed{s_{n^{th}}=u+\frac{1}{2}a(2n-1)}}\]](https://physicsqanda.com/wp-content/ql-cache/quicklatex.com-443b967cc65098d6a1fd661752fcbd05_l3.png)



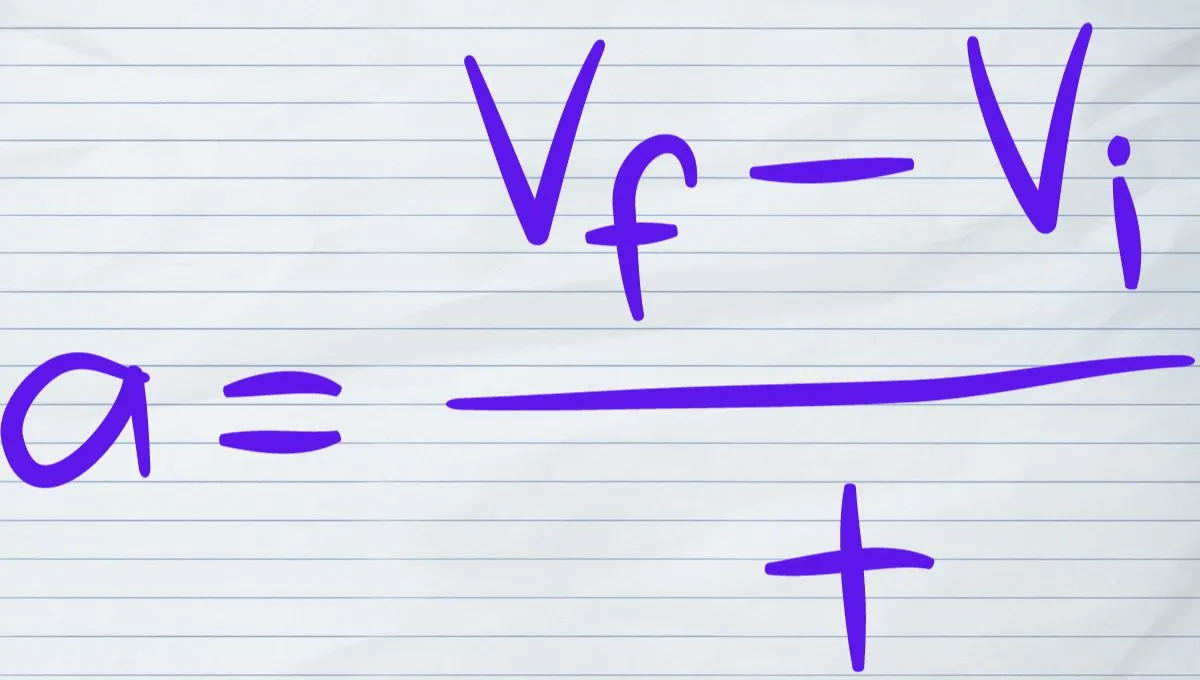

Good luck!