Simple Harmonic Motion Formulas

Spread the love

Simple harmonic motion is a concept in physics that characterizes the oscillatory movement of any body about the equilibrium position. It involves a restoring force proportional to displacement and obeys specific mathematical formulae for its description. This material will delve into the necessary formulas in SHM with explanations and examples and FAQs to clarify understanding.

Contents hide

1 Simple Harmonic Motion Formulas

1.1 Displacement Formula in SHM

1.2 Velocity Formula in SHM

1.3 Acceleration Formula in SHM

1.4 Energy in SHM

2 Table of Key Formulas

3 Frequently Asked Questions

4 Conclusion

Simple Harmonic Motion Formulas

Displacement Formula in SHM

The displacement (x(t)) of an object in SHM is given by:

$x(t) = A \cos(\omega t + \phi)$

Where:

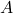$A$ : Amplitude (maximum displacement)
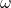$\omega$ : Angular frequency
$t$ : Time
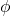$\phi$ : Phase constant

Velocity Formula in SHM

The velocity $v(t)$ is the rate of change of displacement:

$v(t) = -A \omega \sin(\omega t + \phi)$

The maximum velocity is:

$v_{\text{max}} = A \omega$

Acceleration Formula in SHM

The acceleration $a(t)$ is the rate of change of velocity:

$a(t) = -\omega^2 x(t)$

This formula shows that acceleration is proportional to displacement but opposite in direction.

Angular Frequency, Period, and Frequency
Angular frequency relates to the system’s properties:

$\omega = \sqrt{\frac{k}{m}}$

The period (T) and frequency (f) are:

$T = 2\pi \sqrt{\frac{m}{k}}, \quad f = \frac{1}{T}$

Energy in SHM

Total energy (E) is constant, comprising kinetic (K) and potential (U) energies:

$E = \frac{1}{2} m A^2 \omega^2$

Table of Key Formulas

Quantity	Formula	Description
Displacement $(x)$	$x(t) = A \cos(\omega t + \phi)$	Position as a function of time
Velocity $(v)$	$v(t) = -A \omega \sin(\omega t + \phi)$	Rate of displacement
Acceleration $(a)$	$a(t) = -\omega^2 x(t)$	Rate of velocity
Angular Frequency $(\omega)$	$\omega = \sqrt{\frac{k}{m}}$	Depends on spring constant and mass
Period $(T)$	$T = 2\pi \sqrt{\frac{m}{k}}$	Time for one oscillation
Total Energy $(E)$	$E = \frac{1}{2} m A^2 \omega^2$	Total energy in SHM

Frequently Asked Questions

Q1: What is simple harmonic motion?
Simple harmonic motion is a type of periodic motion where an object oscillates around an equilibrium position under a restoring force proportional to its displacement.

Q2: How is angular frequency calculated in SHM?
Angular frequency $\omega$ is determined by the formula:

$\omega = \sqrt{\frac{k}{m}}$

where $k$ is the spring constant and $m$ is the object’s mass.

Q3: What factors influence the period of oscillation?
The period $T$ depends on the mass and the spring constant, calculated as:

$T = 2\pi \sqrt{\frac{m}{k}}$

Q4: What are the energy components in SHM?
The energy in SHM is the sum of:

Kinetic Energy $(K)$ : $\frac{1}{2} m v^2$
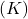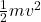
Potential Energy $(U)$ : $\frac{1}{2} k x^2$

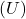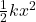
Q5: Can SHM represent real-world systems?
Yes, SHM can model systems such as pendulums, vibrating springs, and certain electrical circuits, making it a versatile concept in physics.

Conclusion

The most fundamental formulas of SHM are the most elementary tools in the study of oscillatory motion in physics. They describe the behavior of systems in terms of displacement, velocity, acceleration, and energy. They provided insight into natural oscillations and mechanical oscillations. Proper mastery of these formulas would help in solving problems in more complex types of oscillations that could be applied in real life.

Simple Harmonic Motion Formulas

Displacement Formula in SHM

Velocity Formula in SHM

Acceleration Formula in SHM

Energy in SHM

Table of Key Formulas

Frequently Asked Questions

Conclusion

Related Posts

Leave a Comment Cancel Reply